Standard deviation is a fundamental statistical concept that measures the variability or dispersion in a data set. Whether you’re a student, professional, or simply curious about statistics, understanding how to calculate standard deviation is an essential skill in your mathematical toolkit. In this article, we will take a deep dive into the world of standard deviation, demystifying the calculations and providing you with a step-by-step guide to conquer this statistical measurement.
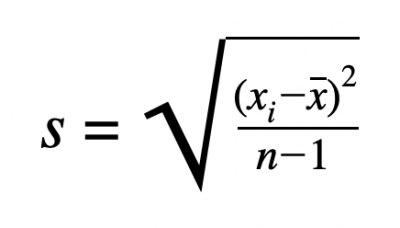
Introduction to Standard Deviation
A standard deviation is a statistical tool used to quantify the spread or dispersion of a data set around its mean. It allows us to determine how closely the individual data points cluster around the average. By calculating the standard deviation, we gain valuable insights into the data’s variability, enabling us to make more informed decisions and draw meaningful conclusions.
Step 1: Calculate the Mean
Before diving into standard deviation calculations, we first need to find the mean (average) of the data set. Add up all the values and divide the sum by the number of data points. The mean acts as a reference point from which we can measure the deviations of individual data points.
Step 2: Calculate the Deviation
Now that we have the mean, we need to calculate the deviation of each data point from the norm. To do this, subtract the mean from each individual data point. The deviations can be positive or negative, depending on whether the data point is above or below the mean.
Step 3: Square the Deviations
We square each deviation to ensure that deviations don’t cancel each other out (since some are positive and others negative). Squaring the deviations allows us to focus on the magnitude of the differences rather than their direction.
Step 4: Calculate the Variance
The variance is calculated by finding the average of the squared deviations. Add up all the squared deviations and divide the sum by the number of data points. The variance represents the average squared distance between each data point and the mean.
Step 5: Take the Square Root
We take the square root of the variance to obtain the standard deviation. The square root ensures that the standard deviation is in the same units as the original data, making it easier to interpret and compare.
Conclusion: Calculating standard deviation is a powerful statistical technique that allows us to understand the variability in data sets. Following the step-by-step guide outlined in this article, you can confidently compute the standard deviation of any data set you encounter. Remember, the standard deviation provides valuable information about the dispersion of data, allowing you to make informed decisions and draw meaningful insights.
Incorporating standard deviation calculations into your analytical toolbox will enhance your understanding of statistical data analysis, making you a more competent mathematician or data scientist. So go ahead, put your knowledge to the test, and calculate standard deviation like a pro!
